はじめに
IT企業では、日常的にABテストが実施され、統計の検定が利用されています。一方で、P値や有意水準が何かよく分からず、作業として検定を利用しているだけの人も少なくなさそうです。そこで、この記事では、統計初心者のマーケターを想定して、有意水準・カイ二乗検定・検出力といった統計の基礎を解説します。IT企業以外でも統計は利用しますし、プロダクトマネージャーにも必要な知識ですので、IT企業のマーケター以外の方にも参考になると思います。
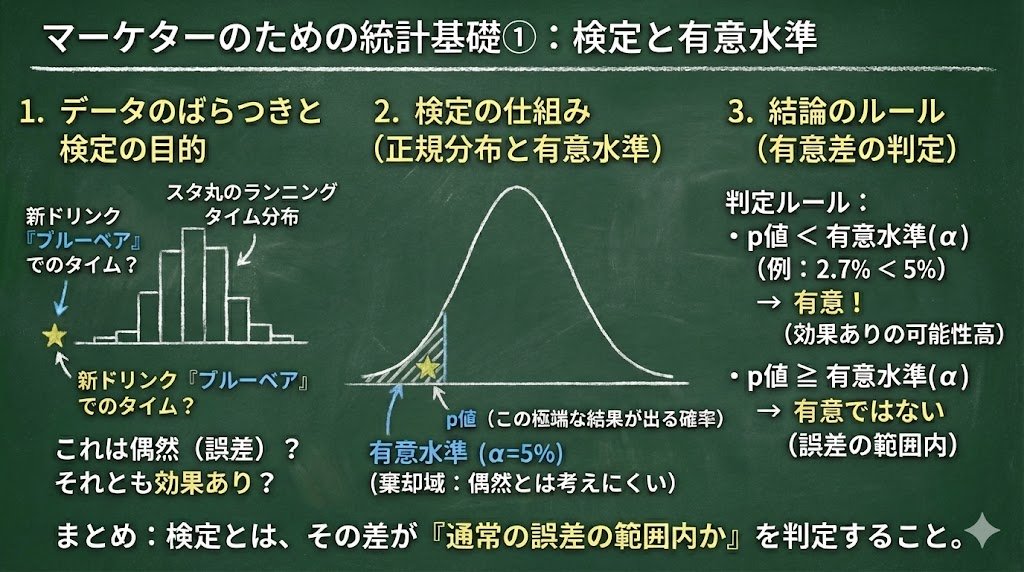
データには散らばりがある
それでは、始めていきましょう。今回は検定について解説していきたいと思います。まず、統計はデータの散らばりを扱う学問であるということを伝えたいと思います。
具体例を挙げながら説明していきます。スタ丸は、メガベンチャーに勤める、25歳のマーケターの男性です。ランニングが趣味で、5kmのタイムを28分4秒、24分52秒・・・と100回計測し、タイム毎の回数をまとめたのが次のヒストグラムです。ヒストグラムの見方は、例えば27分20秒~30秒が9回あったというもので、つまり10秒刻みにしたときの回数をグラフにしたものです。このようにデータは通常散らばります。
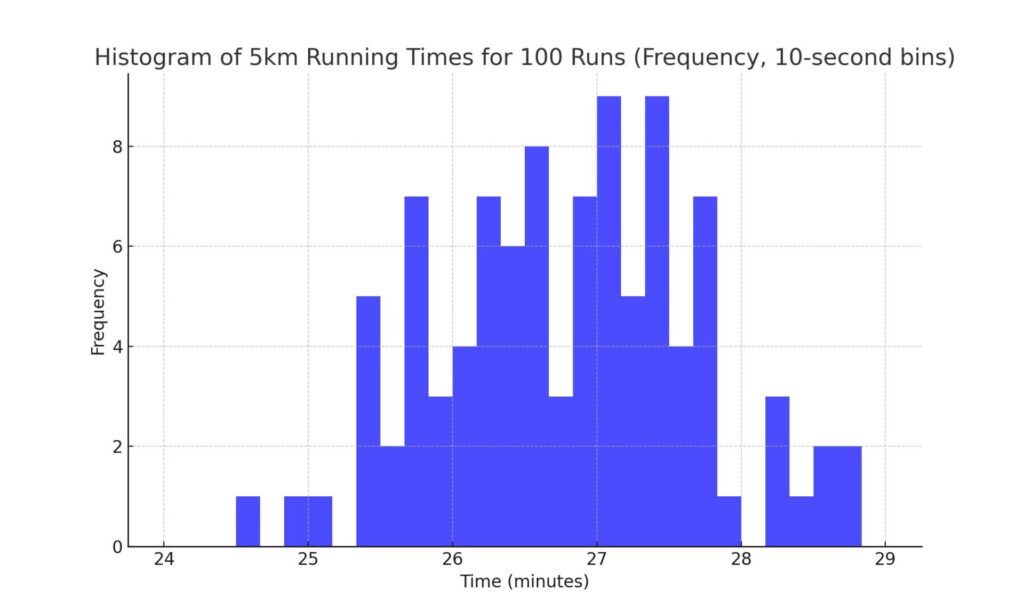
さて、スタ丸は道端で売っている怪しいスペシャルドリンクを見つけました。タイムが早くなるという、その名もブルーベア。翌日、早速ブルーベアを飲んで、5km走ったスタ丸。タイムは24分54秒でした。確かにいつもよりは早いですが、ブルーベアを飲まないときにも、24分台のタイムが出ていることもあります。さて、ブルーベアにはタイムが早くなる効果がある、といえるのでしょうか。
検定で有意かどうかを判定する
ここで、有意性検定の出番です。有意性検定とは、その差が誤差の範囲内か、それとも意味のあるものか(有意であるか)を判定することです。そのために、通常の誤差の範囲というものを考える必要があります。言い換えると、データの散らばりとどのように向き合うか、ということでもあります。例えば、5%の確率でしか起こらないことは、偶然には起きづらいので、効果があるという判定方法です。
具体例で説明していきましょう。スタ丸に(スペシャルドリンクを飲まずに)10000回走ってもらうことを考えてみます。ヒストグラムは以下のとおりです。普通に10000回走ってみて、早いものから5%のタイム(10000回中500番目のタイム。5%点や5百分位点といいます)より早ければ、通常の誤差ではなく、スペシャルドリンクに効果があるという判定方法が考えられます。ブルーベアを飲んだときのタイム(24分54秒)は、5%点の25分9秒より早いので、ブルーベアには早くなる効果がある、といった感じです。
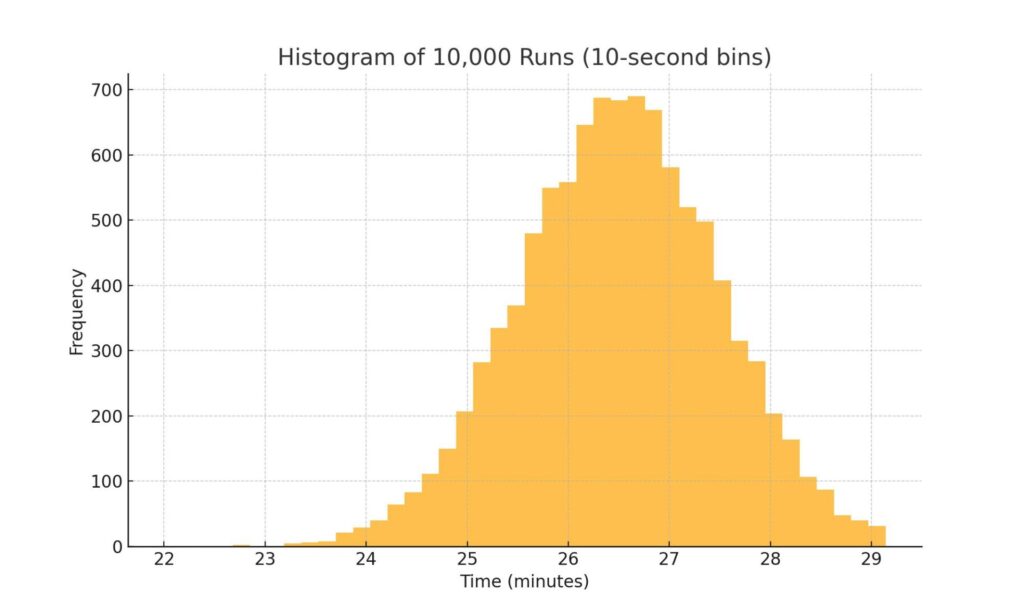
これを検定の言葉に置き換えていくと、スタ丸の5kmのタイムは、10000回の平均が26分49秒、標準偏差は1分。ブルーベアを飲んだときのタイム24分54秒は「ブルーベアに早くなる効果がない」という仮説(棄却したい仮説なので無に帰する仮説、帰無仮説と呼ばれます)を置くと、片側検定のp値が2.7%。有意水準5%と置くと、p値2.7%<有意水準5%なので、ブルーベアにタイムが早くなる効果がある、という判定になります。
有意水準・p値とは何か
少し難しかったと思います。言葉を解説していきましょう。
有意水準とは、検定する人が設定する値(今回だと5%)で、その確率未満で起こったことは偶然ではない、つまり有意であると判断する水準のことです。つまり、5%より早いタイムであれば効果があると判定しよう、というのが、有意水準5%の意味になります。逆にいうと、ブルーベアを飲んでなくても5%の確率で出せるタイムを有意と判定しているため、仮にブルーベアに効果がなかったとしても、5%の確率で「ブルーベアに効果あり」という誤った判定(これを「第一種の誤り」といいます)をしてしまうということになります。
次に、p値(有意確率)とは、その値(今回だと24分54秒)になる確率のことで、p値が小さいほど、あまり起こらないということを意味します。今回のケースだと、ブルーベアに早くする効果がないという仮説の元で、24分54秒になる確率が2.7%でした。なお、ブルーベアのp値2.7%は、平均26分49秒、標準偏差1分のt分布から求めています。
なお、サンプルサイズ(今回だと走った回数)が増えると、正規分布(ガウス分布とも呼ばれます)に近づくという定理(中心極限定理)があります。実際、先ほどの10000回のヒストグラムに正規分布の曲線(黒の太線)を追加すると、よく当てはまっていることが分かります。
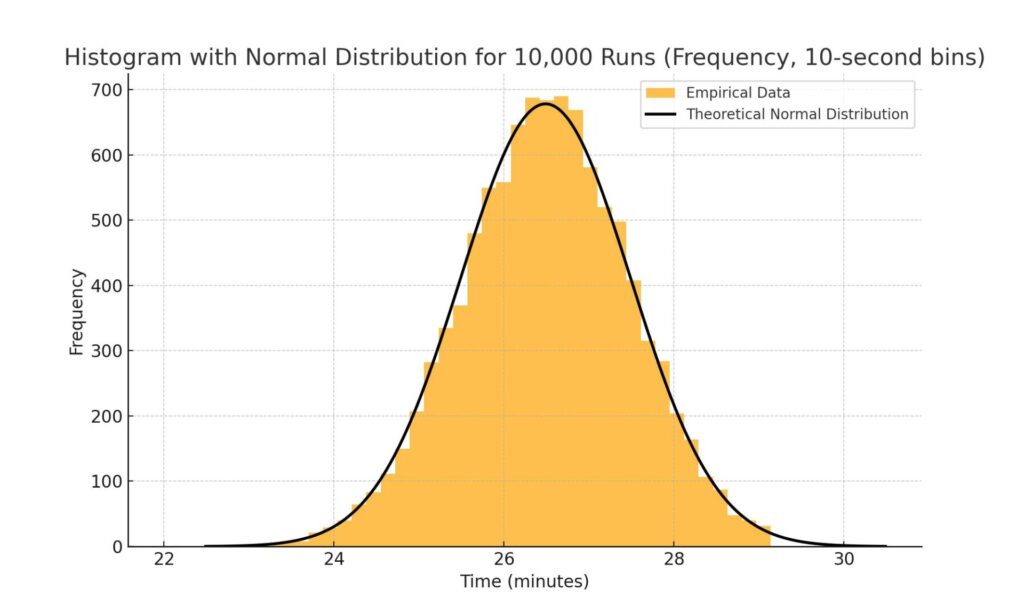
まとめ
今回はここまでです。スタ丸の例で、有意性検定のイメージは伝わりましたか。データには散らばりがあり、通常の誤差か意味のある差かを有意性統計で判定する、通常かどうかのしきい値は有意水準として設定する、というところがポイントです。次回は、マーケティング施策の検証によく使うCVRのカイ二乗検定について解説します。
・有意性検定で、通常の誤差の範囲内か、それとも意味のある差か(有意であるか)を判定
・有意水準とは、その確率未満で起こったことは偶然ではない、つまり有意である、と判断する水準
・p値(有意確率)とは、その値になる確率で、p値≦有意水準で有意と判定






コメント
コメント一覧 (2件)
とても読みやすいしわかりやすかったです!
「…という判定になります。」のところでオワタ/(^o^)\と思ったのですが、すぐに「少し難しかったと思います」と言ってくれて大安堵しました。
「p値ってなんだったっけ…」となりググって難しい説明を頑張って読んで「あ、そうか」となってまた忘れるを繰り返すポンコツなのですがスタ丸くんのおかげでかんたんに理解できました。すごい!
有意水準は基本5%だと思いますが、より正確に結果を出したいとき(医療とか?)には下げるのでしょうか?
初コメントありがとうございます!有意水準を下げることにもメリットと実はデメリットもあり、そこらへんは次のサンプルサイズの記事で書こうと思っていました。