マーケターのための統計基礎②：RCTとカイ二乗検定

はじめに

前回の記事では統計ことはじめとして、検定と有意水準について説明しました。今回は、マーケティング施策の検証でよく使うABテスト（RCT）、そしてカイ二乗検定について解説していきます。一部、言葉が難しく感じるかもしれませんが、結局こうすればいいよというHowも説明しますので、ぜひ付いてきてください。

バナーの効果を検証する

では、いきましょう。前回も登場したスタ丸は、メガベンチャーでスマートフォン向けゲームのマーケティングを担当しています。今度、ゲームのリニューアルに合わせて大規模にWeb広告を打つことが決まっており、Googleディスプレイ広告用に、2種類のバナーを作成しました。さて、どちらのバナーの方が効果があるかをどのように検証したらいいのか、というのが今回のお題です。

結論から先に話すと、スタ丸は、ユーザーをランダムに2分割するABテストを実施しました。バナーAは985ユーザーに表示されて、ゲーム登録が32ユーザー、ゲーム登録ユーザー数を表示ユーザー数で割ったコンバージョンレート（以下、単に「CVR」）は3.25%でした。バナーAとバナーBの結果をまとめたものが以下の表になります。バナーBの方がCVRは約1.5倍高いですが、カイ二乗検定の結果、p値が7.69%となり、有意水準5%で有意な差があるとはいえないという判定になりました（詳細は後述します）。

RCT（ランダム化比較試験）

さて、スタ丸が実施したことのポイントを解説していきましょう。1点目はテスト方法についてで、スタ丸は、ユーザーをランダムに2分割するABテスト、を実施しました。これは、ランダム化比較試験や無作為化比較試験、Randomized Controlled Trial（RCT）と呼ばれるテスト方法です。

RCT以外の方法だと、例えば、時期をずらして、まずはバナーAをテストして、次にバナーBをテストして、両者を比較する前後比較があり、それなりに利用されている印象です。しかし、前後比較には難点があり、例えばバナーBをテストした時期に大型キャンペーンを実施していてCVRが高くなっていた場合、バナーの良し悪し以外のキャペーンの影響で、バナーAとバナーBを適切に比較することができません。これは一例ですが、このように前後比較の場合、前後の期間で同質性を担保できず、適切な検証ができない可能性があります。

次に、違う方法を考えてみます。同時期にバナーAとバナーBをテストし、バナーAを女性に、バナーBを男性に表示すれば、適切に検証することは可能でしょうか。この方法も適切な検証にならない可能性があります。なぜなら、仮に（バナーに関わらず）そもそも女性よりも男性の方がCVRが高い場合、バナーBのCVRが高い結果だったとしても、CVRが高い理由が男性だからか、それともバナーBがよかったからかの要因を切り分けることができないためです。

ここでは、性別について記載しましたが、他にも年代、エリアなどが、CVRに影響を与えるかもしれません。このように、特定の要因によって生じる誤差のことを「系統誤差」と呼びます。この系統誤差はどのように避けることができるのか、その答えが、今回スタ丸が利用したRCT、ランダム化比較試験になります。具体的に何をするかというと「ユーザーをランダムに（無作為）に分ける」それだけです。それによって、性別や年代など、バナー以外の要因をほぼ同質にし、系統誤差の影響を小さくすることができます。他の要因を排除するために、シンプルだけど、めちゃめちゃ強力、それがRCTです。

このランダム化（無作為化）は、ロナルド・フィッシャーが確立した実験計画法の3原則の一つで、ロナルド・フィッシャーは、イギリスのロザムステッド農事試験場の統計研究員として研究を続け、1935年に「The Design of Experiments（実験計画法）」を出版し、実験計画の礎を築いた方です。

RCTのより詳細な説明については「いちばんやさしい、医療統計」をご覧ください。

CVRにはカイ二乗検定を利用する

解説ポイント2点目は、バナーAとバナーBに効果の差があるかを検定したカイ二乗検定についてです。ユーザー登録のように登録したか登録しないか、つまりユーザー登録が1か0の値を取るものについては、カイ二乗検定で独立性を検定することができます。ここは理解するというよりも、そういうものだと一旦受け入れてしまった方が早いと思います。少しだけ補足すると、独立とは「バナーAとバナーB」と「ユーザー登録の有無」に関係がないということを意味して、独立性がない＝バナーAとバナーBの効果に差がある、と考えます。カイ二乗検定を含め、検定したいこと（検定内容）と検定方法の対応表を記載しておきます。

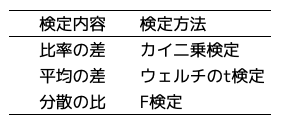
実際に、カイ二乗検定する方法も説明していきましょう。「検定実務」（この記事の著者が無償で提供しているサービス）にアクセスして「比率の差」のタブをクリックします。使い方はカンタンで、A群-訪問数に分母（表示ユーザー数）、A群-CV数に分子（登録ユーザー数）を入力し、B群も同様に入力します。そうすると、カイ二乗検定の結果が右側に出力されます。なお、有意水準はデフォルトが5%になっているので、20%に変更する場合には0.2と入力してください。今回のバナー検証の結果は以下のとおりで、有意水準5%でバナーAとバナーBの効果に有意な差があるとはいえない、という判定でした。

カイ二乗検定の計算方法は「いちばんやさしい、医療統計」をご覧ください。独立性の検定に関する他の事例は「統計Web」が参考になります。

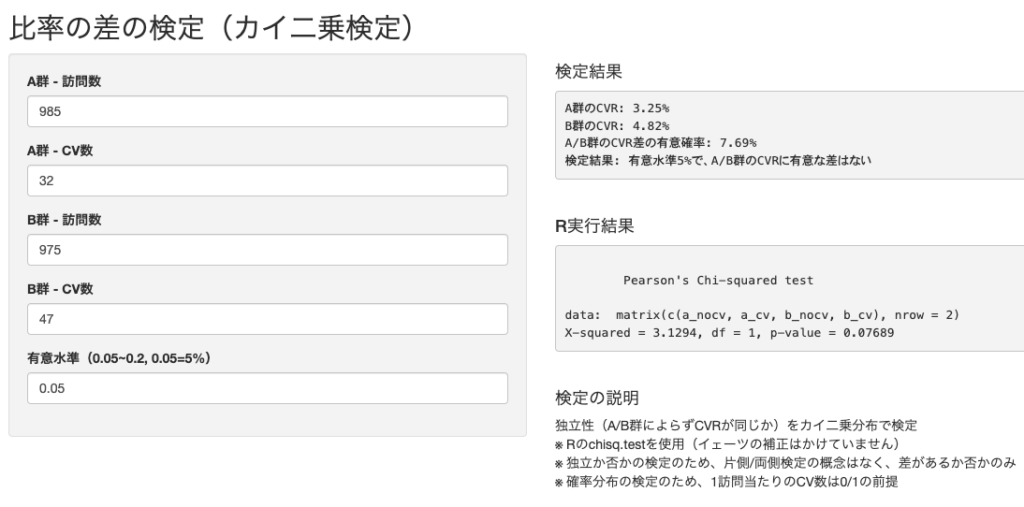
有意差がないときのネクストアクション

有意な差がなかったときのネクストアクションについても考えてみましょう。選択肢はいろいろあるのですが、例えば、①バナーBをさらに改善、②テスト期間を伸ばして改めてカイ二乗検定、が挙げられるでしょう。有意差を出すための要素である、改善幅を大きくする、サンプルサイズ（今回のケースでは表示ユーザー数）を増やす、にそれぞれ対応した選択肢です。さて、今回のABテストの結果を受けて、スタ丸はどうするのでしょうか。

まとめ

今回はここまでです。マーケティングの実務でよく使うRCTとカイ二乗検定について解説しました。前回の記事と今回の記事で、マーケティングの実務で使う統計の基礎の基礎ぐらいは押さえられたと思います。それぐらいRCTとカイ二乗検定はよく使います。次回は、検定の誤りと検出力、必要なサンプルサイズの求め方について書こうと思っています。それでは！

・他の要因を排除するために、RCT（ランダム化比較試験）を利用
・1か0の値を取るの登録比率の差の検定については、カイ二乗検定を利用
・カイ二乗検定には検定実務を利用可能