マーケターのための統計基礎③：検証に必要なサンプルサイズと検出力

2024年8月15日2024年8月16日

はじめに

さて、今回は検証に必要なサンプルサイズについてです。難しい内容ですが、具体例を挙げて、なるべく分かりやすく解説していきたいと思います。サンプルサイズを説明するために、確率密度、仮設検定の第一種・第二種の過誤、検出力といった内容にも触れていきます。

最終的には、マーケティングの実務でよく使うCVRのカイ二乗検定に必要なサンプルサイズの算定がこの記事のゴールなのですが、平均の検定の方がグラフでイメージしやすいですので、統計基礎①のランニングタイムで話を進めていきます。

再びランニングの話

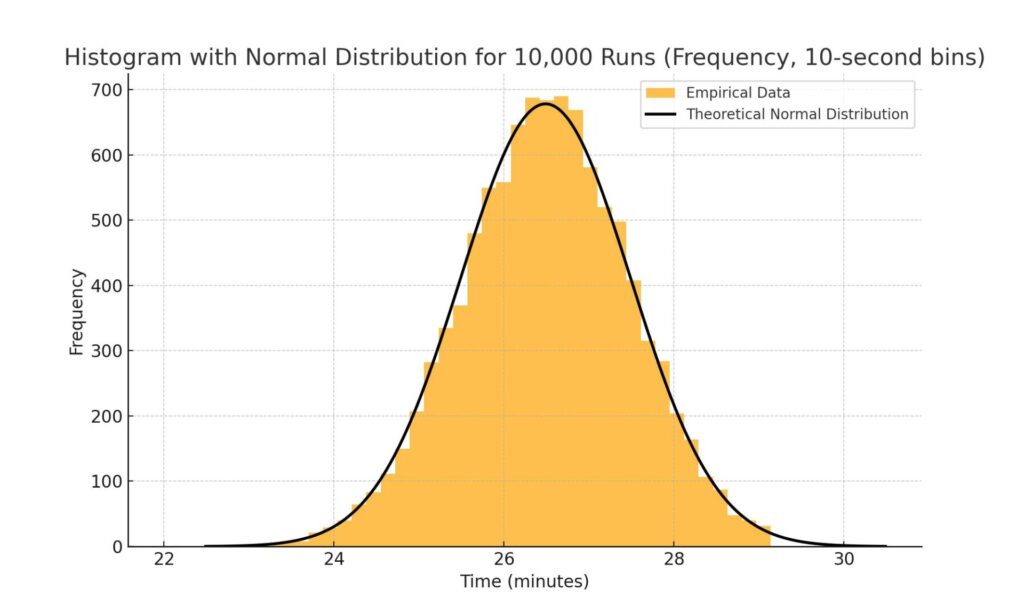
統計基礎①は、スタ丸の5kmランニングのタイムを例に、道端で売っている怪しいスペシャルドリンク「ブルーベア」に効果があるかを検定しました。その時のヒストグラム（10000回走って、10秒区切りのタイムごとの回数をカウントしたもの）がこちらです。スタ丸の5kmランニングタイムは平均26分49秒・標準偏差1分で、黒の線は正規分布です。

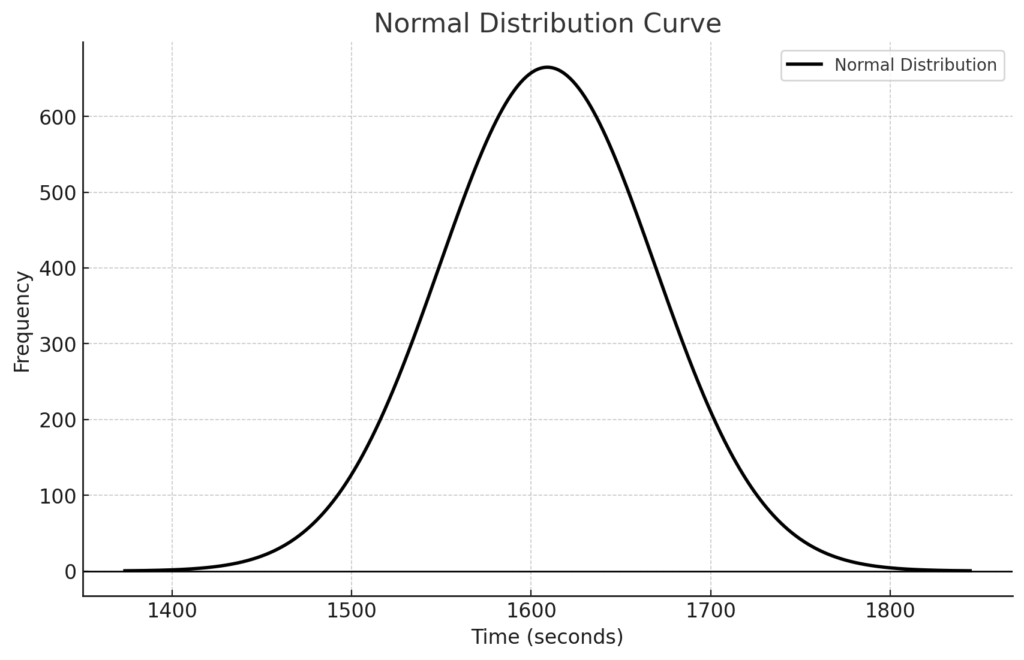
このグラフからヒストグラムを削除して、正規分布だけを残します。横軸は分を秒に修正しました。平均が26分49秒ですので、1609秒になります。

次に、縦軸を「10秒区切りのタイムごとの回数」から確率密度に変更します。確率密度は「ある範囲にデータがどれだけ集中しているか」を示すもので、確率密度の高さ自体に意味はなく、特定の範囲の面積が確立を示します。分かりづらいと思うので具体例で説明していきましょう。

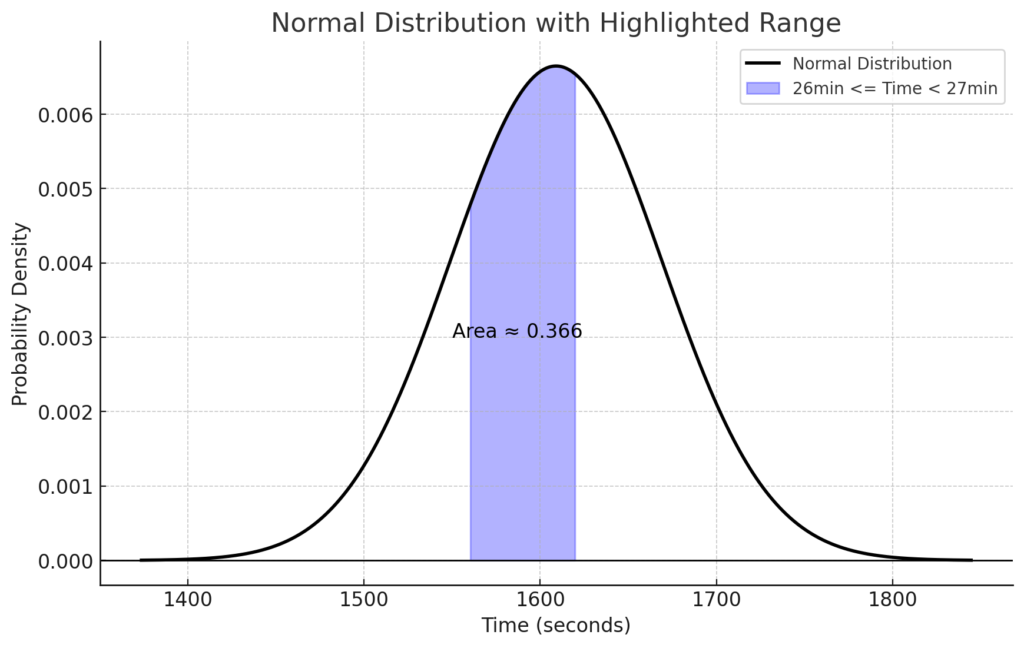
上のグラフの青色部分は、26分以上27分未満の範囲を示しています。青色部分の面積(確率密度を積分したもの)は0.366で、36.6%の確率でスタ丸の5kmタイムは26分以上27分未満になる、ということを意味します。実際、1万回走ったときのタイムでは、26分以上27分未満の範囲に該当する回数は3,626回で、1万回×36.6%=3,660回と近しい回数になっていることが確認できます。なお、3,626回と3,660回の差はデータの散らばりですね。

ブルーベアの本当の効果

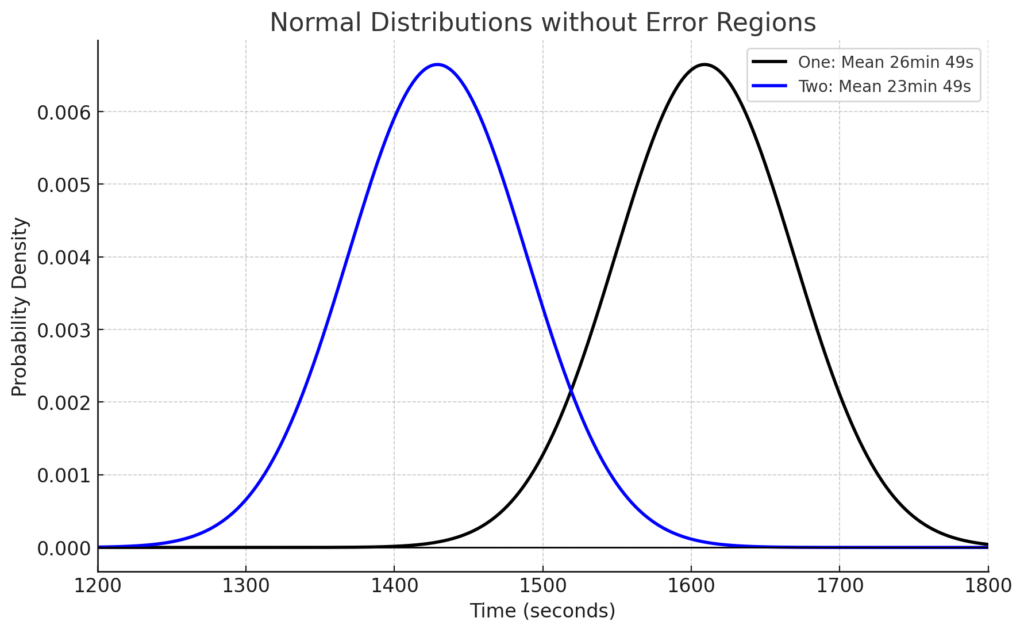
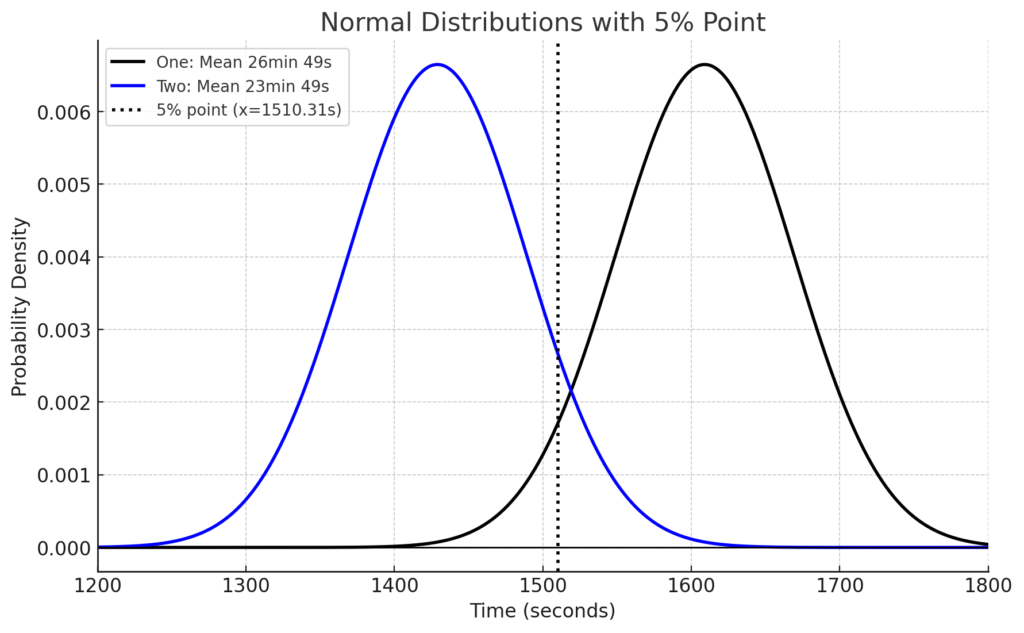
スペシャルドリンク「ブルーベア」には3分タイムを短縮する効果があると仮定します。つまり、スタ丸の通常の5kmタイムは平均26分49秒だったので、ブルーベアを飲めば平均23分49秒になる、という仮定です。標準偏差は、ブルーベアを飲んでも飲まなくても1分のままとします。この時に、ブルーベアを飲んだときの5kmタイムの正規分布を青線で追加したものが以下です。黒線の正規分布を左に180秒（3分）だけ移動させたものが、ブルーベアを飲んだときの正規分布になります。

統計基礎①では、片側検定で有意水準5%と置きました。そこで、下側5%点の1510秒（25分10秒）のところに点線を追加します。前回はブルーベアを飲んだときのタイムが24分54秒（p値2.7%）だったので、有意差検定の結果、p値2.7%<有意水準5%となり、ブルーベアにタイムが早くなる効果がある、という判定になりました。

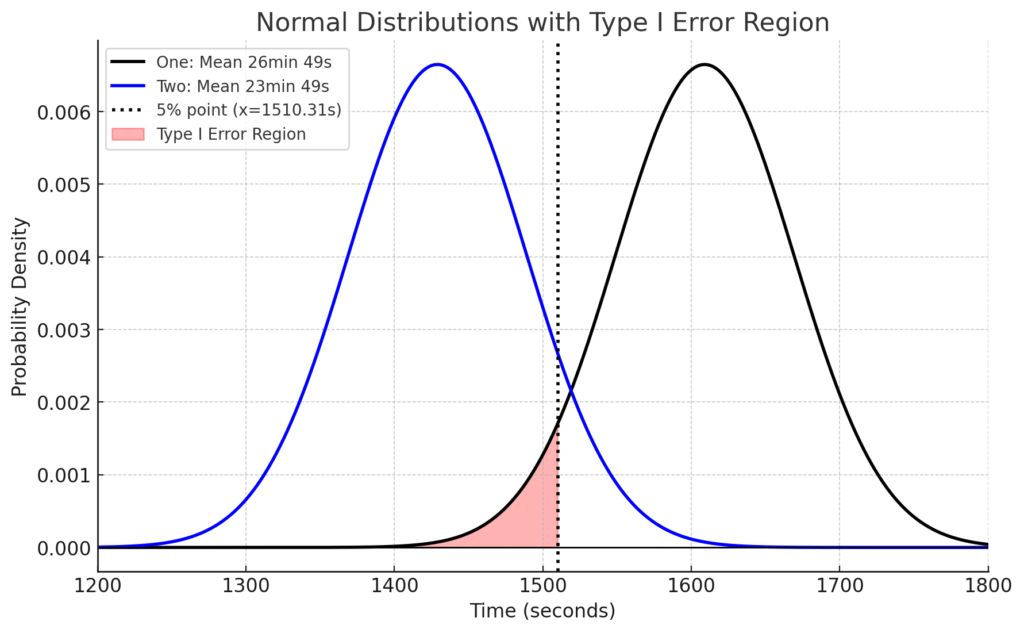
仮説検定の過誤

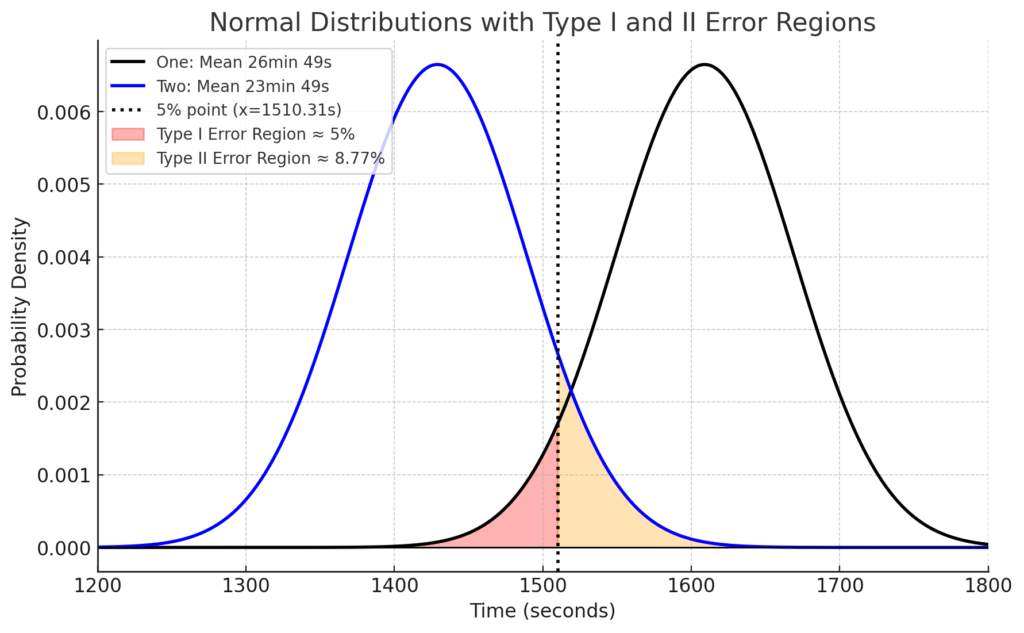
仮設検定における誤り、つまり過誤には2種類あります。まずは「第一種の過誤」。次のグラフで赤い範囲は、黒線の正規分布（ブルーベアを飲まない通常のタイム）のうち、下側5%点以下の範囲です。この赤い範囲が何かというと、仮にブルーベアに効果がなかったとしても、「ブルーベアに効果あり」という誤った判定（これを「第一種の過誤」といいます）をしてしまう範囲です。

つまり、第一種の過誤とは、本当は効果がないのに効果ありと判定してしまう誤りで、その可能性は有意水準と同じ割合になります。言い換えると、片側検定の有意水準5%とは、通常の下側5%点よりも早いタイムであれば効果ありと判定するという意味なので、効果がなかったとしても5%は「効果あり」と誤って判定してしまうということです。

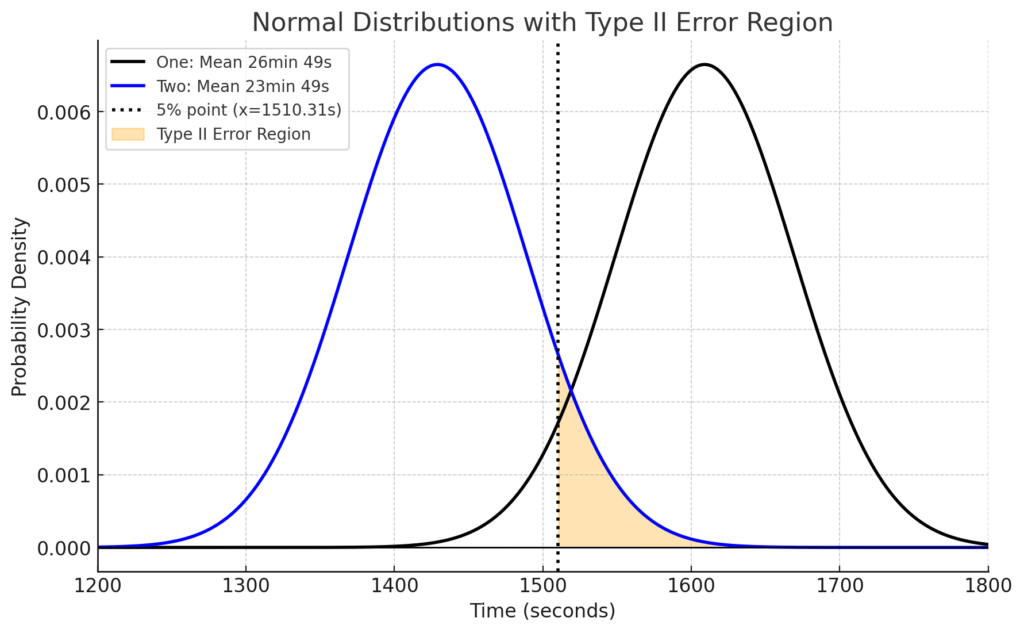
次に「第二種の過誤」です。第二種の過誤の範囲は、下のグラフの黄色部分で、青線の正規分布（ブルーベアを飲んだときのタイム）のうち、黒線の正規分布（ブルーベアを飲まない通常のタイム）の下側5%点以上の範囲です。この範囲は、本当はブルーベアに効果があるのに、片側検定の有意水準5%で「効果ありと判定できない」範囲です（統計検定の性質上、効果なしということができません）。つまり、本当は効果があるのに検定で効果ありと判定されない誤りで、これが「第二種の過誤」です。下のグラフで黄色部分の面積は8.8%です。逆に、実際に効果があり検定で効果ありと判定できる割合を検出力といい、今回のケースだと100%から第二種の過誤の8.8%を引いた残りの91.2%が検出力ということになります。

第一種の過誤と第二種の過誤を以下のようにまとめることができます。本当は効果がないのに検定で効果ありと判定してしまうのが「第一種の過誤」。違う言い方をすると、本当は効果がないのに、検定で「ブルーベアに早くなる効果がない」という帰無仮説（棄却したい仮説なので「無に帰する仮説」ということで、帰無仮説と呼ばれます）を棄却してしまう、つまり、効果ありと判定してしまう誤りです。逆に、本当は効果があるのに、検定で帰無仮説を棄却できず、効果ありと判定できないのが「第二種の過誤」です。

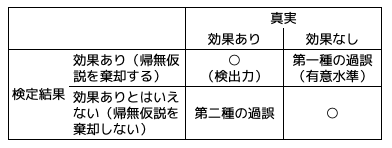
有意水準は、表を縦方向に見て、真実が効果なしを分母にして、検定結果が効果あり（第一種の過誤）を分子にした割合（今回のケースだと5%）。また、検出力は、真実が効果ありを分母にして、検定結果が効果あり（第二種の過誤を除いたもの）を分子にした割合です（今回のケースだと91.2%）。

有意水準と検出力の関係

繰り返しになりますが、有意水準5%とは、本当は効果がないのに効果ありと判定してしまう誤りが5%あるということです。その誤りというかリスクをどこまで許容するかという水準ともいえます。一見、この誤りは小さければ小さいほどよいことのようにも見えます。そこで、有意水準1%のケースをグラフにしたものが以下になります。

有意水準を1%に減らしたことによって、効果ありと判定するラインは左側に移動し、第一種の過誤の割合は5%から1%に減少しましたが、逆に第二種の過誤の割合は8.8%から25.0%まで増加してしまいました。このように、第一種の過誤と第二種の過誤の割合は、効果ありと判定するラインの位置によって、どちらかを減らすとどちらかが増えるという関係にあります。

検証に必要なサンプルサイズ

さて、いよいよ、検証に必要なサンプルサイズについての説明です。まずは、よく間違えられるサンプル数を含めて、サンプルサイズの定義を説明したいと思います。一言でいうと、サンプルサイズとはデータの量のことで、サンプル数とはデータセットの数のことです。少しイメージしづらいと思いますので、具体例で説明すると、統計基礎②のようなバナー効果検証で3群に分けてABテストを実施し、全群まとめた表示ユーザー数が3000だったケースでは、サンプルサイズは3000、サンプル数は3になります。ここでは、検証に必要なデータ量を算出したいので「検証に必要なサンプルサイズ」が正しい言い方になります。

次に、サンプルサイズが大きくなることで何が嬉しいのかという話です。統計基礎①では、スタ丸はブルーベアというスペシャルドリンクを飲んで「1回」走り、そのタイムが24分54秒でした。1回ではなく、4回ブルーベアを飲んで走って4回の平均値でブルーベアの効果を検定するとどうなるでしょうか。詳細な説明は省きますが、4回の平均値の標準誤差は、5kmランニングタイムの標準偏差の1/2になります。このときのグラフが以下になります。

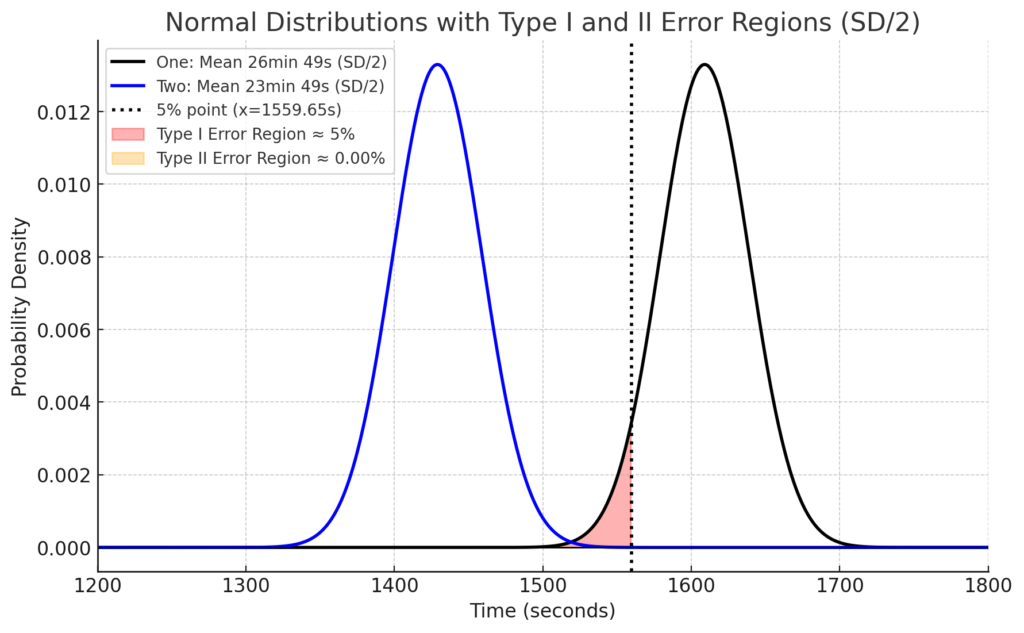
正規分布の標準誤差が半分になったことで、横幅が縮まり、第一種の過誤（赤い部分）は有意水準5%のままですが、第二種の過誤（黄色い部分）は8.8%から0.00066%まで下がり、検出力は91.2%からほぼ100%まで上がりました。つまり、サンプルサイズを大きくすることで、標準誤差が小さくなり、第二種の過誤が小さくなり、検出力が上がります。

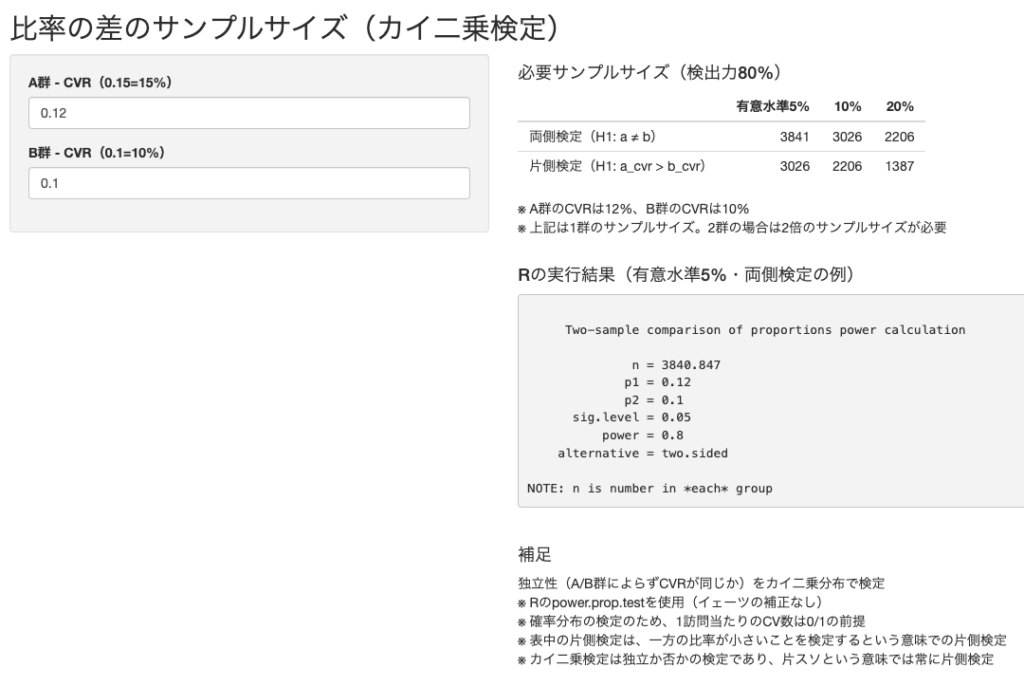
ここまで説明して、改めて、検証に必要なサンプルサイズの求め方です。マーケティングの実務でよく使うCVRのカイ二乗検定の場合、検証に必要なサンプルサイズは、効果の大きさ・有意水準・検出力を与えると、算定することができます（平均の差の検定の場合には、効果の大きさに加えて分散も必要になります）。通常のバナーの効果が10%、改善後のバナーの効果が11%と見込まれるときに、両側検定で有意水準5%・検出力80%であれば、1群に必要なサンプルサイズは3,841となり、2群合計で7,682のデータ量が必要になる、という感じです。

違う説明を試してみると、カイ二乗検定の場合、サンプルサイズ・効果の大きさ・有意水準・検出力の4つはセットで、他の3つが分かればもう1つが求められるという関係です。例えば、サンプルサイズ・効果の大きさが分かっていて、有意水準5%と設定すれば、そのときの検出力が求められます。その前提になっているのが、これまで説明してきたように、有意水準を小さくすれば検出力が下がり、サンプルサイズが大きくなれば検出力は上がるといった関係です。

説明は難しかったと思いますが、 A/B群のCVRのカイ二乗検定に必要なサンプルサイズ自体は、ツールを使って簡単に求めることができますのでご安心ください。「検定実務」（この記事の著者が無償で提供しているサービス）にアクセスして「サンプルサイズ」のタブをクリックします。A群 – CVRとB群 – CVRに想定しているCVRをそれぞれ入力すれば、以下のように検出力80%のときに、有意水準5%~20%までのサンプルサイズが表示されます。